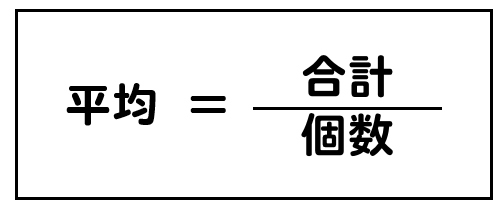
平均値のみが与えられても、 全体の平均値を求められない! ということです。 ※上の問題では、行きと帰りの道のりが同じという条件があるため、 平均値を求められたのです。 今回は、世の中でよく使われる「平均」について、 平均を求めるために、まずは合計値を出しましょう。 ab312=ab6 このように合計値を求めたら、5人で割ってあげればよいので (ab6)\div5=\frac {ab6} {5}(点) このように平均を表すことができます。 答え \frac {ab6} {5}(点) (2)男子5人の平均点は x 点、女子3人の平均点は y 点でした。 このとき男女合わせた8人の平均点を表しなさい。ツイート 無料ダウンロード・印刷できる小学5年生の算数平均の求め方練習問題プリント です。 いくつかの量や数から全体の平均を求める練習ができます。 平均の求め方(1) 答え 平均の求め方(2) 答え 平均の求め方(3) 答え

中1数学 平均値 と 中央値 例題編 映像授業のtry It トライイット
平均 値 求め 方 中学
平均 値 求め 方 中学- 偏差値の計算方法は複雑で難しい ? ※偏差値の求め方に関する疑問を解決しよう まず結論から言ってしまうと、偏差値は「(自分の得点-平均点)÷標準偏差×10+50」という公式で求められる。 そう聞いて、「なるほど、なるほど」と思った数学が得意な高校生ももちろんいるだろうがの (2)について, (2) 修正によって,平均値が, 161−1608=02 (cm) 大きくなっているので,(∗)のデータのいずれか1つが, 02×5=1 (cm) だけ大きくならなければならない。 ・・・・・・ (★) また,修正後のデータの中央値が162cmとなることにより, 156,160,161



平均値の求め方を教えてください あと 画像の平均値の求め Yahoo 知恵袋
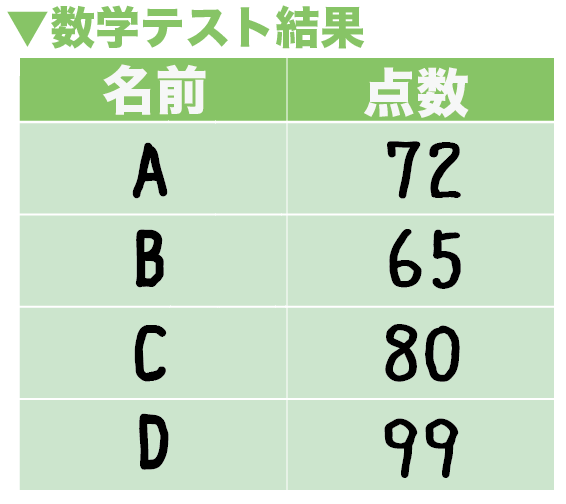
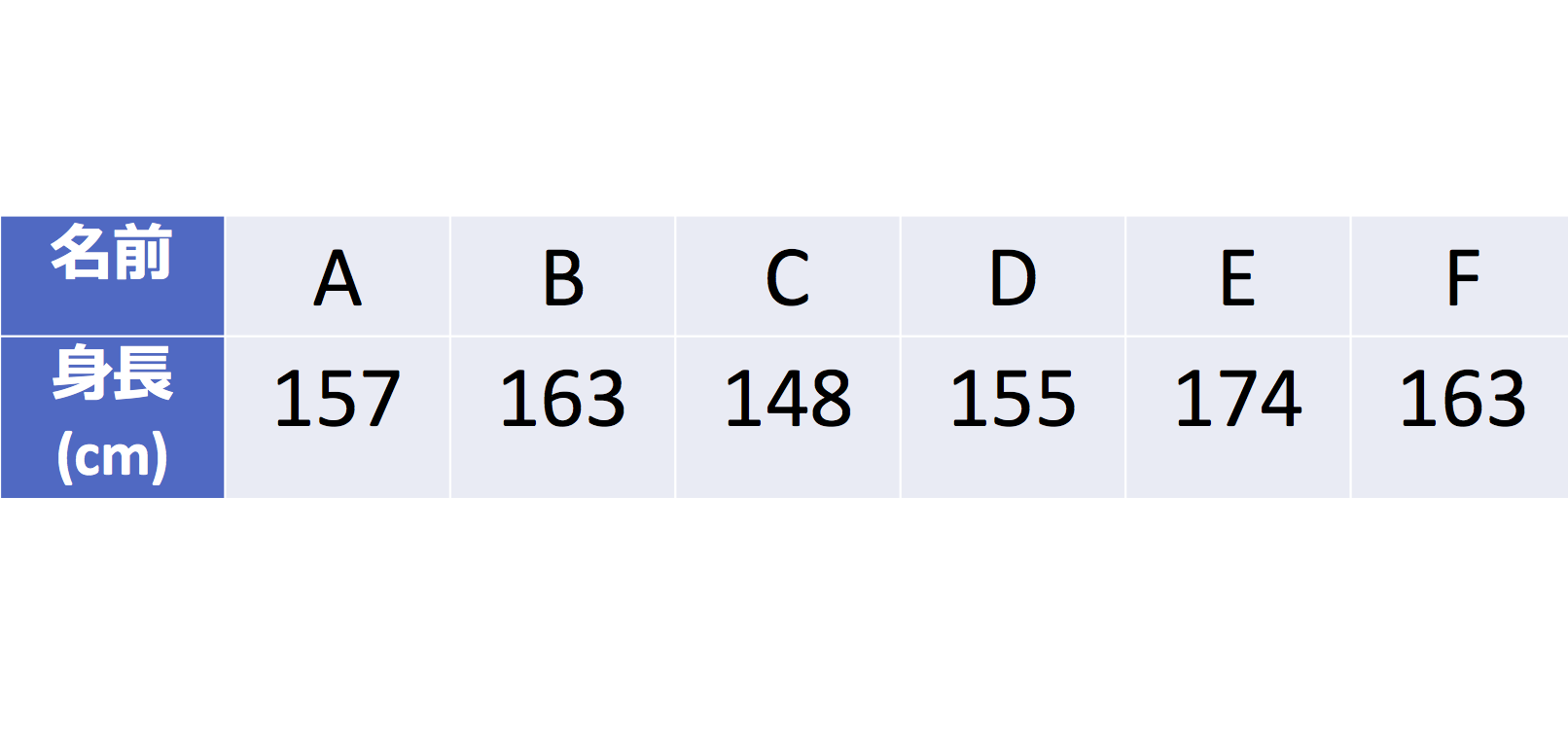
ヒストグラムから平均値を求める方法 新元号『令和』... どんな時代になるのでしょうか。 さて! 昨日は、平均値の考え方をお伝えしました。 ①真ん中の数値ではないこと! ( 等分してるってこと。 ) ②全部の合計から割ること!中学入試の算数で出題される平均算について例題と解き方の解説をしています。 中学受験レベルになると単純に平均を求める計算だけでなく、いろいろなパターンの平均算が出てきます。例えば、 平均値から全体の数を求める計算 などがあります。 平均値の求め方は ①:データをすべて足す ②:①で求めた値をデータの個数で割る でしたね。 よって、求める平均値は ()÷4 = 166(cm)・・・(答) となります。
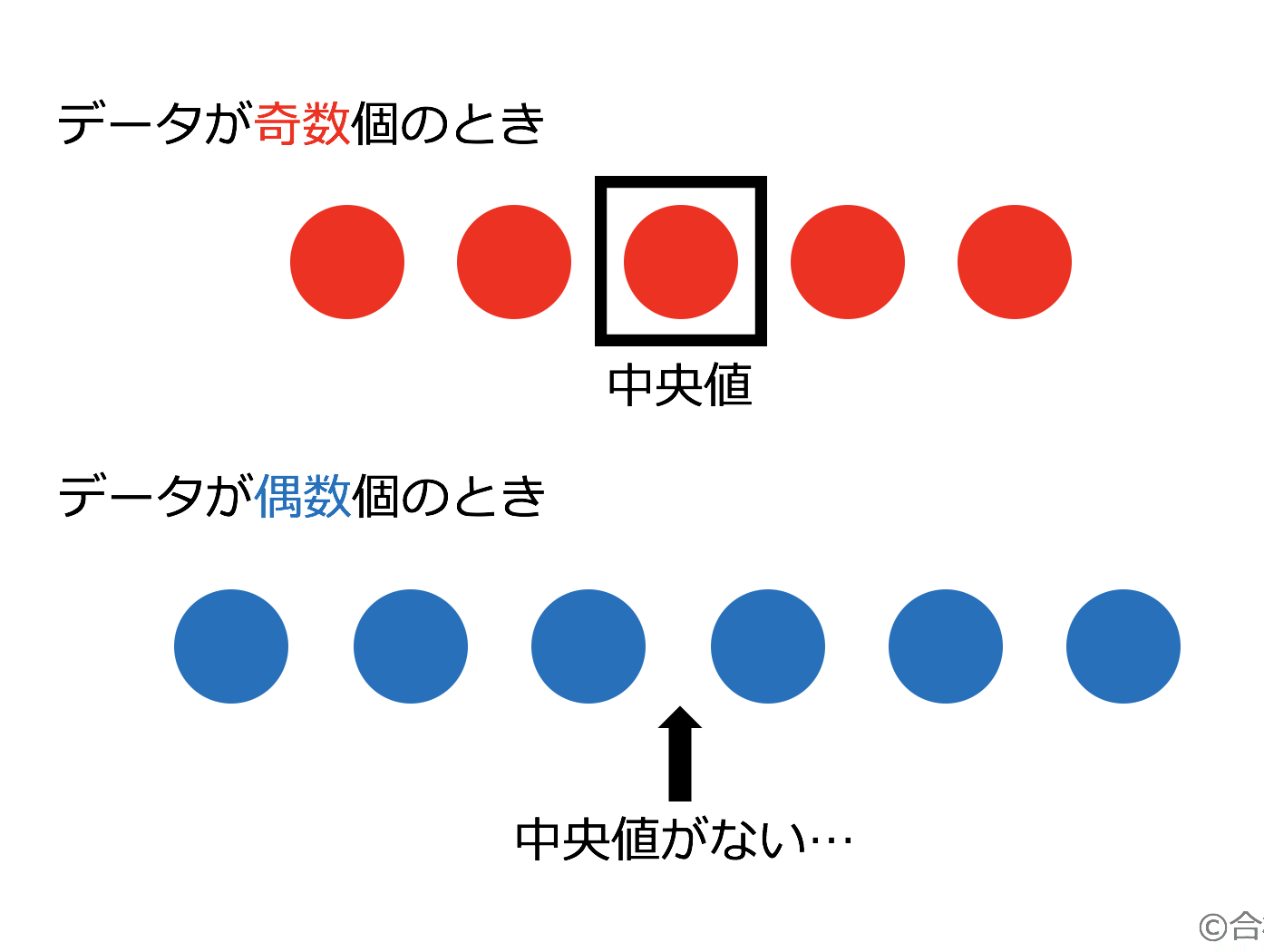
中央値の求め方(奇数) データの数が奇数個の場合には、ちょうど真ん中に位置する値を見つけることができます。 そのため、真ん中に位置する値が何番目になっているのかを求めることができれば、すぐに中央値が分かりますね! 中央値は何番目 中1数学 平均値 と 中央値 練習編 映像授業のtry It トライイット ヒストグラムを使った平均値の求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく 小学5年生の算数 平均の求め方 練習問題プリント ちびむすドリル 小学生 ヒストグラムから平均値を「仮の平均」という考え方を用いると、平均値を出すための計算が楽になることがあります。 ますは、簡単な例で「仮の平均」の意味を学習しましょう。 例 \(43,48,41\) の平均を求めなさい。 もちろん平均値は \(()÷3=44\) です。
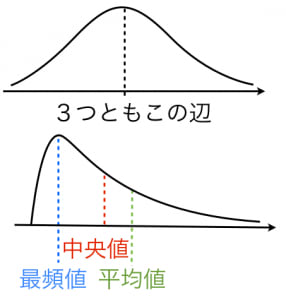
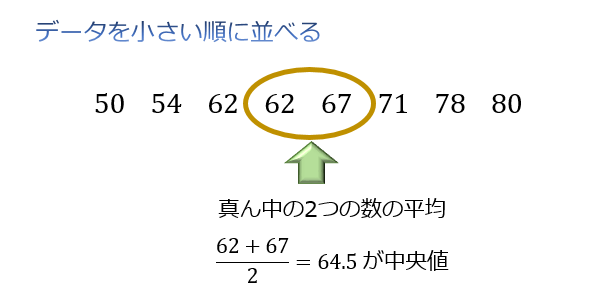
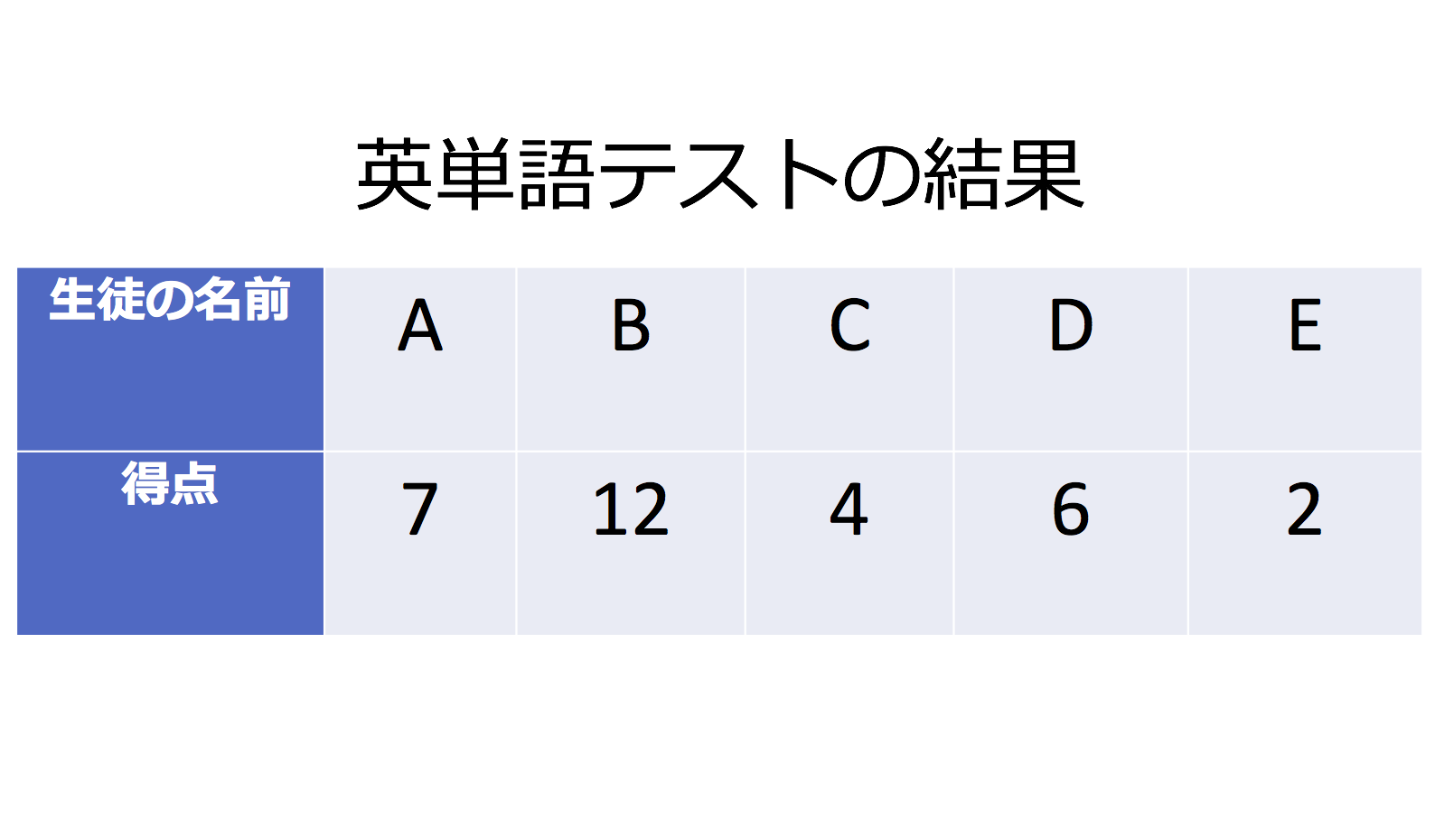
平均の求め方は「全てのテストの点数を足して、教科数で割る」でしたね。 よって、\\displaystyle \frac{ }{ 5 }=66(点)\となります。 平均の求め方は以上です。 最後に平均値を求めることのメリット、デメリットを紹介しておきます。 平均値、中央値、最頻値の求め方や計算方法を紹介してきました。 まとめると、 平均値各データの値の総和をそのデータの個数で割ったもの 中央値データを小さい順に並べた時、ちょうど中央にある値のこと 最頻値最も頻度の高いデータのこと解き方 解くにあたって、 「5回分の平均の長さ」、これを求めることでAB間の距離が推定できる ことを理解しておきましょう。 つまり、(10.12+9.98+10.2+10.03+10.11)÷5=10.0 これが答えになります。 母集団 , 平均 , 母集団の平均 , 『中学数学




度数分布表を完成させよう 求め方は決まっている 苦手な数学を簡単に




中学数学 平均値と中央値の3つの違い Qikeru 学びを楽しくわかりやすく
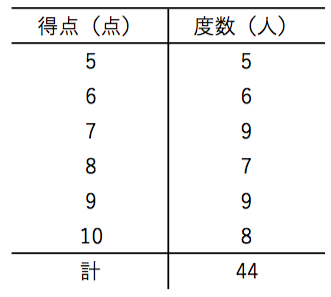
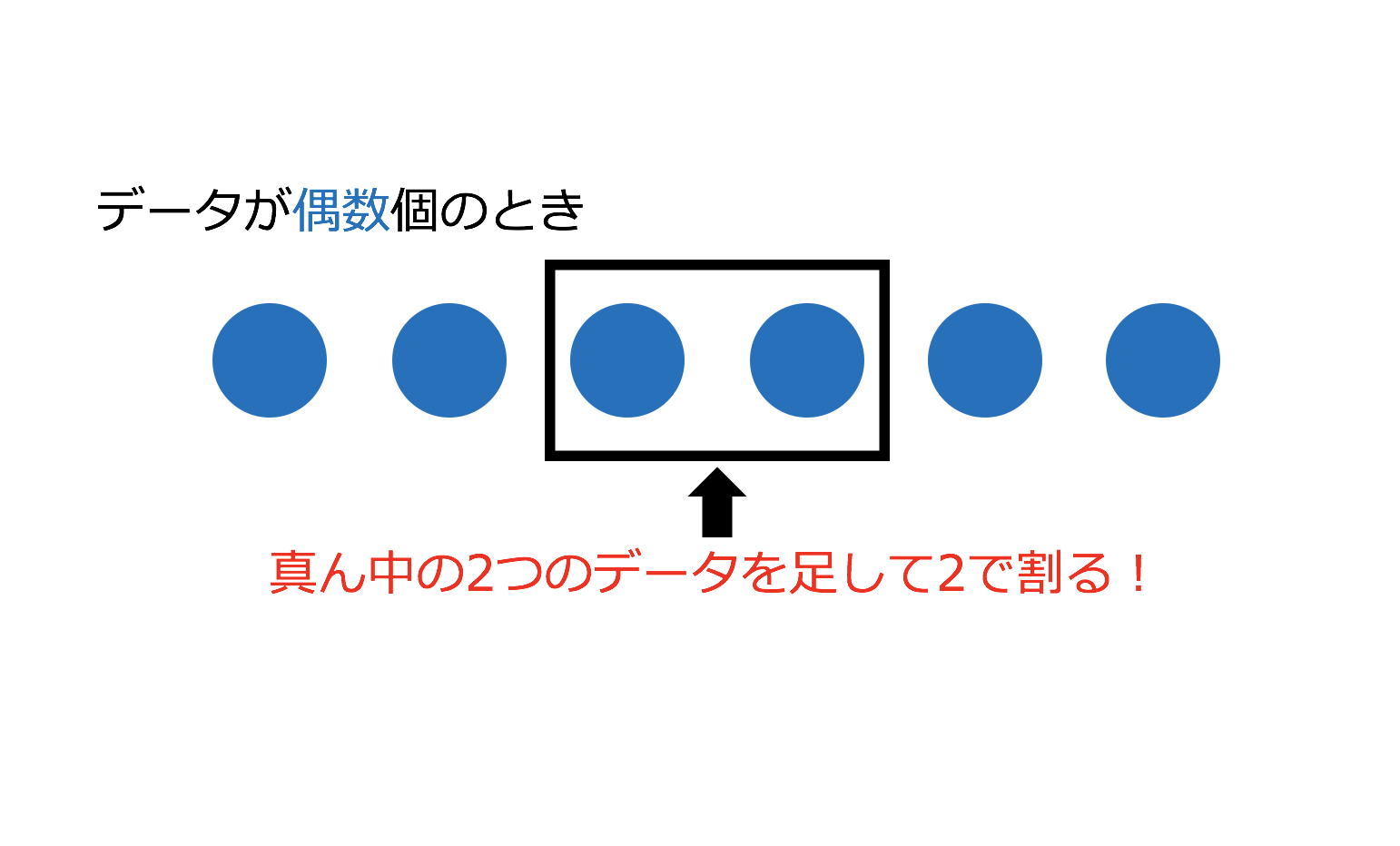
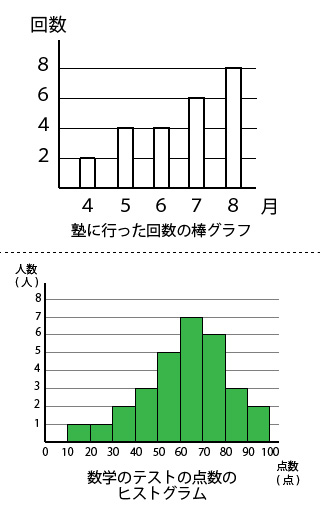
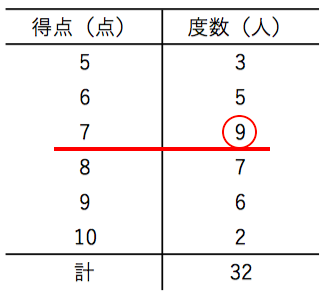
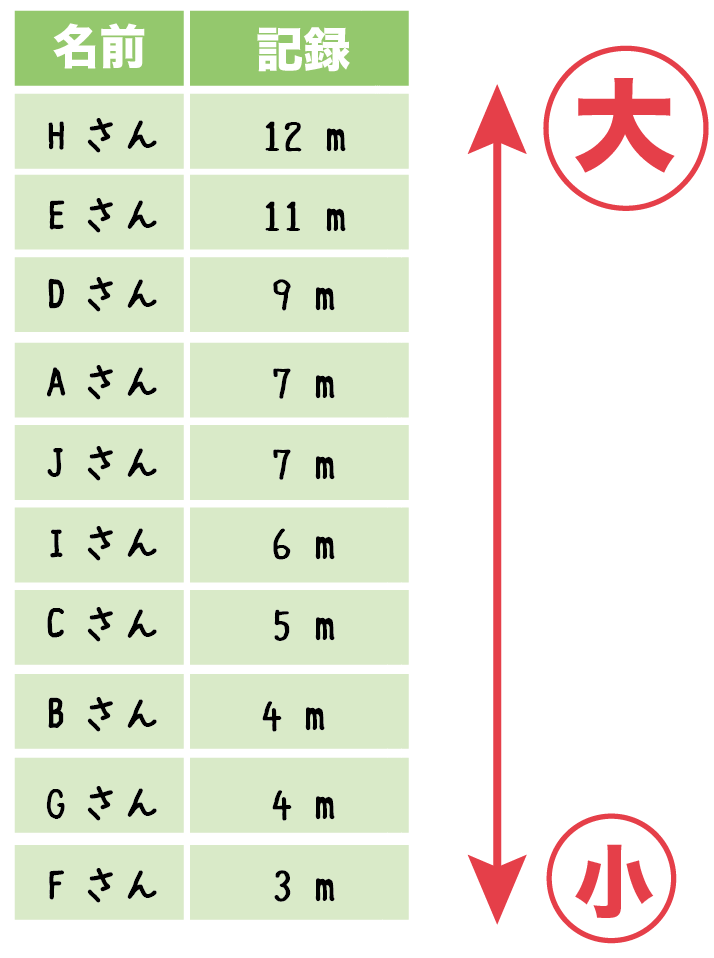
代表値には 「平均値」「中央値」「最頻値」「範囲」 などがあります. 「真理は1つだけでなければならない」などと決めつけてはいけません.どの代表値も長所短所があり,各自が資料を使って分析したいときに,ねらいを実現するために一番適した「平均値」は、すべてのデータを たし算 して、全体の 12で割れば 求められるね。 「中央値」は、真ん中の人の値だよ。12人のうちの真ん中だから、6番目と7番目の人の間。6番目と7番目の人の値を足して2で割れば「中央値」が出せるね。中1数学『資料の整理と分析』のところでの平均値の求め方は2パターンです。 一つは小学校のときからのおなじみの平均値の求め方です。 平均値: 個々の資料の値の合計を資料の総数で割った値 もう一つが、度数分布表から平均値を求める求め方です。
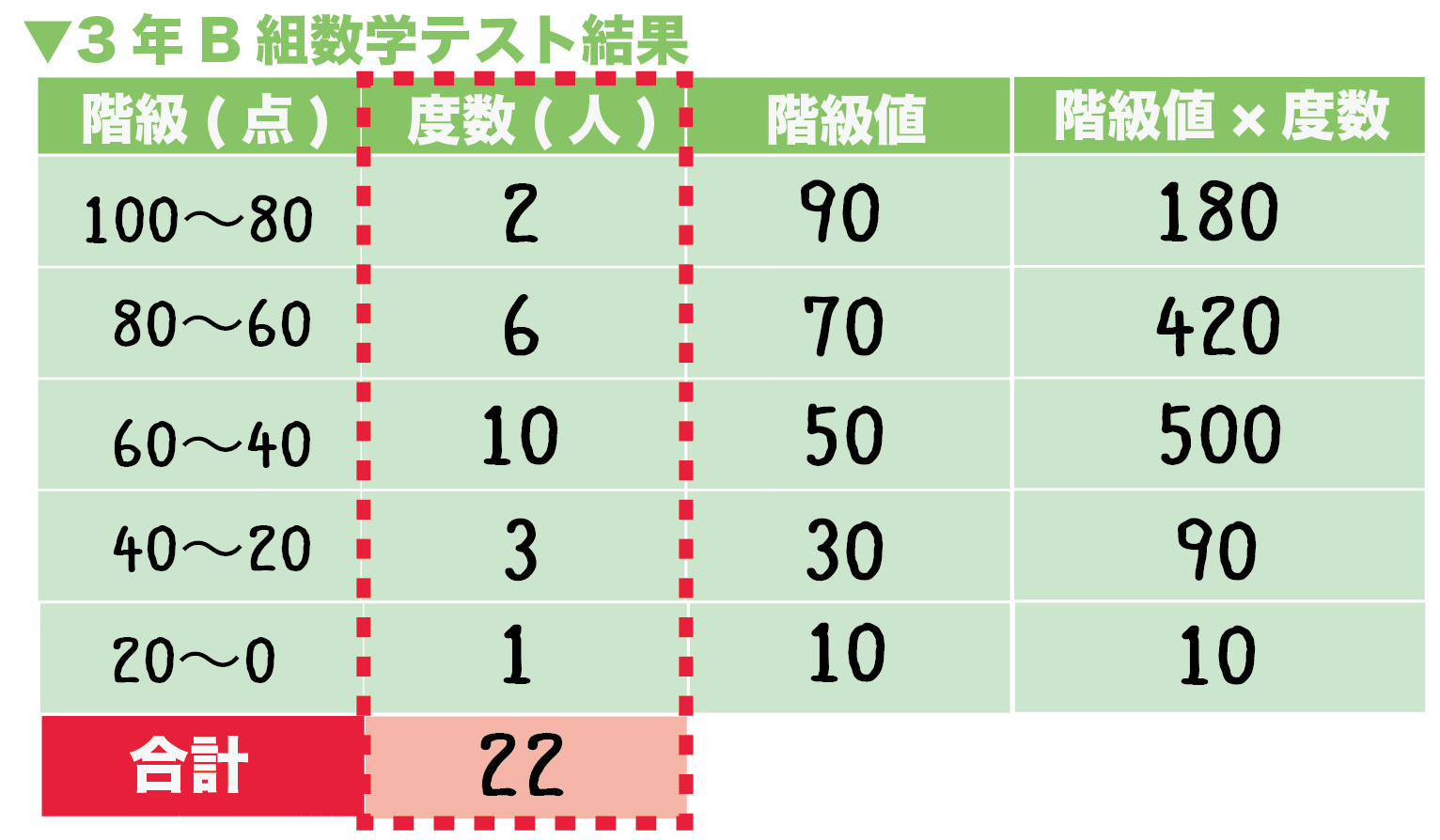



度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




中学数学 3分でわかる 平均値の出し方 Qikeru 学びを楽しくわかりやすく
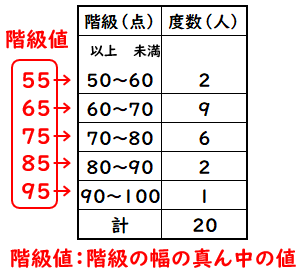
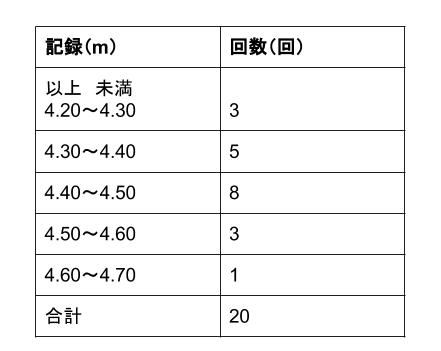
度数分布表から平均値を求めるときは,その階級の真ん中の値(階級値)を使います。 つまり,50点以上60点未満の4人の点数はすべて55点とみなすのです。 この階級値を使うと,「55点が4人,65点が2人,75点が2人」ということになり,平均値はこれらの合計を全体の人数でわるという考え方になります。 以上により,平均値は625点と求められます。 中央値の求め方 では、問題を通して中央値の求め方を確認してみましょう! 次の資料において中央値を求めなさい。 まずは、データを大きさの順に並べます。 小さい順、大きい順はどちらでも良いですが、小さい順で並べかえるのが一般的です 分散の正の平方根を計算して「標準偏差」が求められる。 step05 「平均との差」を「標準偏差」で割る 自分の点数から平均点を引いた値を、標準偏差で割る。 step06 「偏差値」を求める step05で出た数値を10倍してから50を足すと偏差値が求められる。



平均値の求め方を教えてください あと 画像の平均値の求め Yahoo 知恵袋
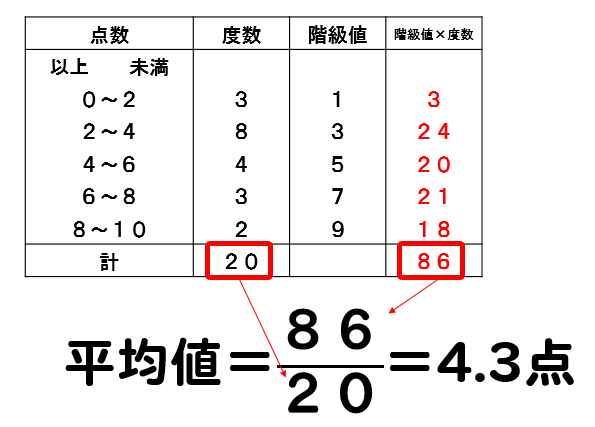



フレッシュ 平均 値 求め 方 中学
偏差値=50+ (自分の得点-平均点)÷2 実はこれだけで、偏差値の目安がわかります。 たとえばあなたが、社会で60点を取ったとします。 その時の社会の平均点が70点だとしたら、 偏差値は約45になる ということです。 私は教師時代、 この方法で何人かの生徒の偏差値を 計算してみたことがあるのですが、 コンピューターを使って計算した正確な偏差値と ~平均の求め方~ $$平均=合計\div 個数$$ ~合計の求め方~ $$合計=平均\times 個数$$標準偏差分の点数を取ると、偏差値は10アップするので、平均点の60点+10点である70点は偏差値60。 仮に70点からさらに10点高い80点を取れば偏差値は70となります。 (70-60)÷10×10+50=偏差値60 (80-60)÷10×10+50=偏差値70 上記の式を言葉に変換してみると、 (自分の得点-平均点)÷標準偏差×10+50=自分の偏差値 になります。 ちなみに、 塾
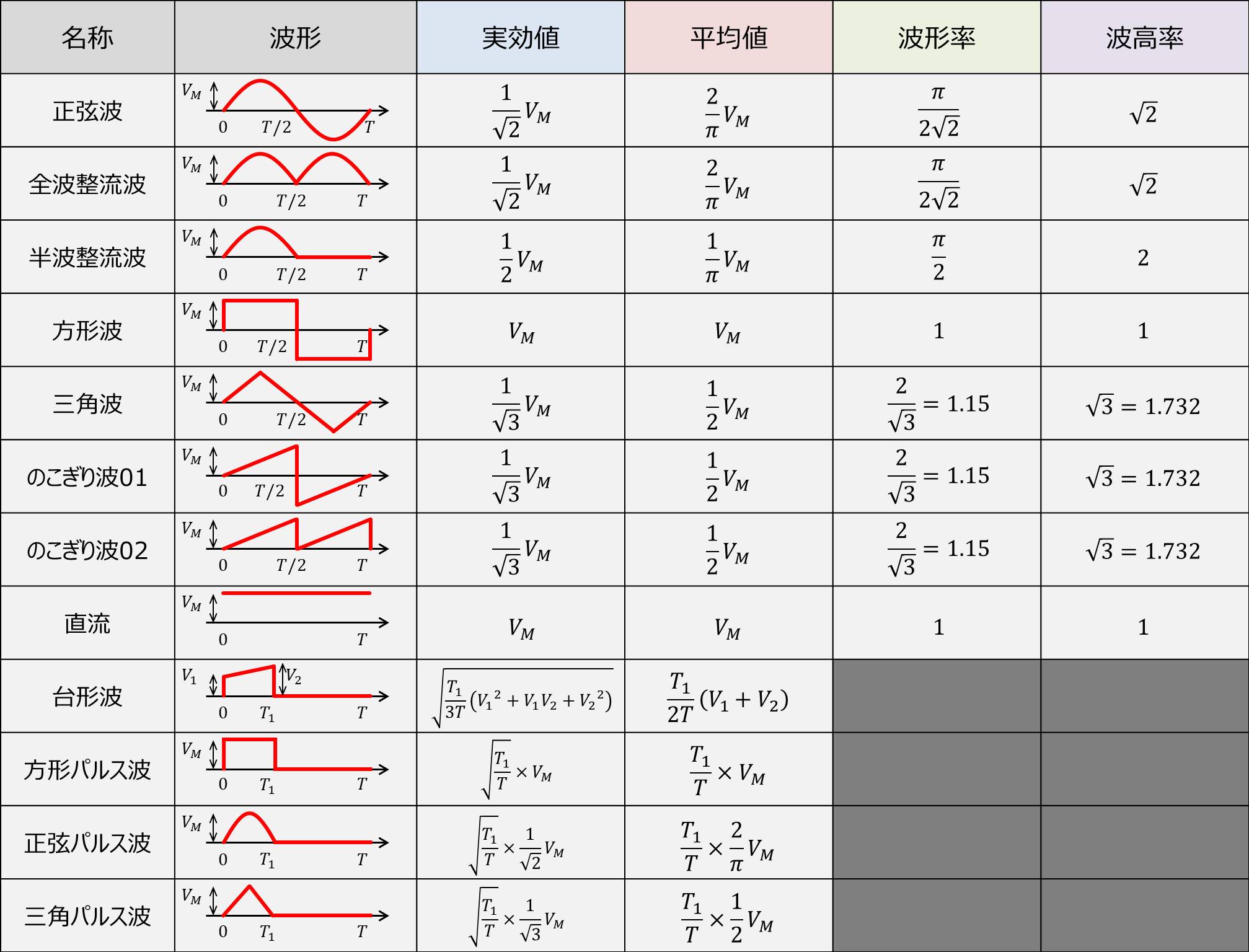



様々な波形の 実効値 平均値 波形率 波高率 のまとめ Electrical Information




標準偏差とは何か その求め方や公式の意味 使い方をわかりやすく説明します アタリマエ
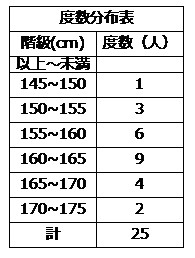
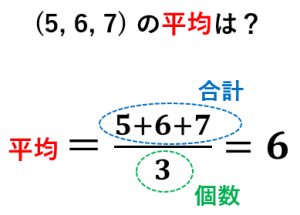
3分でわかる!平均値の出し方 を伝授しますよ! 中学数学で大活躍!平均値の出し方 あるデータにおける平均を求める式は、 です。「データの値をすべてたしたもの」を「データ数」でわればいんですね! たとえば、期末テストの平均点を出してみましょう。階級値と度数分布表での平均の求め方中学1年数学 問題をノーヒントでやってみよう 答えをチェックしよう 156.5cm 攻略ポイントを確認しよう ・代表値とは、資料全体の特徴をつかむための数である。 ⇒平均値=合計÷数 ⇒階級値=その階級の 平均値とは 求め方が一瞬でわかる 中央値との違いも解説 高校生 度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを 度数分布表から平均値と最頻値を求める 苦手な数学を簡単に 中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数



中学数学について質問です この問題が分かりません 1 右 Yahoo 知恵袋




中1数学 最頻値 と 階級値 練習編 映像授業のtry It トライイット
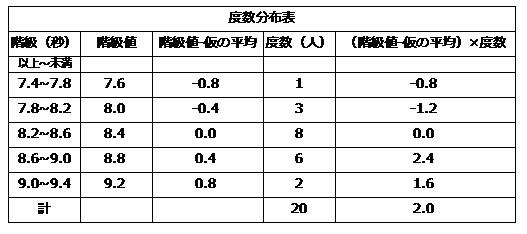
偏差値の計算式に、求めた標準偏差値をはめ込みます。 偏差値=(得点-平均点)÷標準偏差×10+50 (80-70)÷816×10+50=622 aさんは、今回のテストで偏差値622だったことがわかります。 偏差値は最高100点? 偏差値に最高値や最低値はありません。解き方 (階級値)×(度数)は次のようになる。 平均値= {(階級値)×(度数)}の合計 度数の合計 = 960 =48 (cm) 答 48 cm 考え方 45 cm 以上 50 cm 未満の階級値 47 5 cm を仮の平均とする。 平均値=仮の平均+ {(階級値-仮の平均)×(度数)}の合計




平均値 中央値 最頻値の求め方といくつかの例 高校数学の美しい物語




正負の数の利用 平均を求める Youtube



Q Tbn And9gct9g81v6fbuxe2zy40zobgjz7pv4jyf9dpik7xrlwfhfckmjg0k Usqp Cau




中1数学 平均値 と 中央値 例題編 映像授業のtry It トライイット




度数分布表での平均値の求め方 仮平均も 高校数学 Youtube



Math 平均値と仮の平均 働きアリ




平均値とは 求め方が一瞬でわかる 中央値との違いも解説 高校生向け受験応援メディア 受験のミカタ




中学数学 平均値と中央値の3つの違い Qikeru 学びを楽しくわかりやすく




中1数学 平均値 と 中央値 例題編 映像授業のtry It トライイット




中1数学 資料の活用 平均値の求め方 Youtube



Studydoctor平均値と仮平均での求め方 高校数学 Studydoctor



1



Math 平均値と仮の平均 働きアリ



平均値について 苦手な数学を簡単に



Studydoctor階級値と度数分布表での平均の求め方 中学1年数学 Studydoctor



3分で分かる 平均値 中央値 最頻値の求め方をわかりやすく 練習問題つき 合格サプリ



Math 平均値と仮の平均 働きアリ




3分で分かる 平均値 中央値 最頻値の求め方をわかりやすく 練習問題つき 合格サプリ




中1数学 平均値 と 中央値 練習編 映像授業のtry It トライイット



平均値 中央値 最頻値の求め方といくつかの例 高校数学の美しい物語




平均値 中央値 最頻値の求め方といくつかの例 高校数学の美しい物語



小学6年生の問題です これの中央値の求め方がよくわかりません 出来れ Yahoo 知恵袋




資料のちらばりと代表値 度数分布表からの平均値の求め方 中学数学 定期テスト対策サイト




中学数学 平均値と中央値の3つの違い Qikeru 学びを楽しくわかりやすく



統計データの分析で使われる平均値 中央値 最頻値 もう一度やり直しの算数 数学



度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




度数分布表から平均値を求める 中学1年の数学 身勝手な主張




小学6年生の算数 資料の調べ方 度数分布表 柱状グラフ 練習問題プリント ちびむすドリル 小学生



3分で分かる 平均値 中央値 最頻値の求め方をわかりやすく 練習問題つき 合格サプリ



資料の整理 平均値の求め方を理解しよう インターネット家庭教師のアスミラ




小6 算数 小6 35 平均とちらばり Youtube




最頻値とは わかりやすく



中央値と四分位数の求め方 四分位範囲 四分位偏差とは何か アタリマエ



平均の求め方 計算式 と意味 欠点 具体例で学ぶ数学



中学数学 平均値求め方 下の画像の求め方が分からないので教えてください Yahoo 知恵袋




小5 算数 小5 21 平均 Youtube



2




高校生は知るべき評定平均値の付け方と計算



Math 平均値と仮の平均 働きアリ




データの分析 平均値 中央値 最大値 最小値 範囲 最頻値




中学数学 平均値と中央値の3つの違い Qikeru 学びを楽しくわかりやすく



1



中央値を求める 中学から数学だいすき




中央値の求め方 二つあることもある Avilen Ai Trend




3分で分かる 平均値 中央値 最頻値の求め方をわかりやすく 練習問題つき 合格サプリ




中央値の簡単な求め方みたいなのがあったら教えて頂きたいです Clear
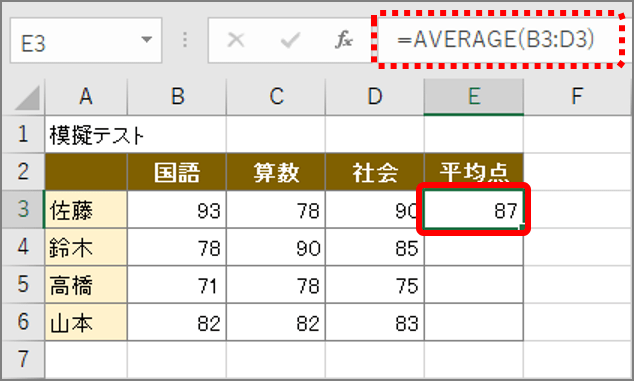



エクセル 平均 を簡単に求めよう いまさら聞けない平均算出ワザ3選 Getnavi Web ゲットナビ




求め方が分かりません 教えてください Clear




中学 1年 数学 この資料の平均値の求め方を教えてください 中学 1年 数学 教えて Goo




例題 平均値と仮平均 Youtube




中1 数学 資料の整理4 平均値と中央値 12分 Youtube




中1数学 資料の活用 平均値の求め方 Youtube



度数分布とは 表や多角形の作り方 平均値 中央値 最頻値の問題 受験辞典



代表値 平均値 中央値 最頻値 の意味と違い 数学fun




高校数学 分散 とは 練習編 映像授業のtry It トライイット




中学1年数学 正の数 負の数の応用 基準からの平均 Youtube



ヒストグラムの平均値の求め方教えて下さい ヒストグラムから Yahoo 知恵袋




平均値 中央値 最頻値はどう使い分ける 3つの代表値を詳しく解説 遊ぶ数学




身長の平均値の求め方を教えて頂きたいです Clear



ヒストグラムから求める 平均値 中央値 最頻値 苦手な数学を簡単に



中学数学 度数分布表 ヒストグラム 中学数学の無料オンライン学習サイトchu Su




中1数学 資料の活用 平均値の求め方 Youtube




小5算数の宿題 仮の平均 を使って平均を求める方法 がんばるブラザーズ



平均値 中央値 最頻値の違い 求め方 使い分け 計算問題 受験辞典



中学数学 平均値と中央値の3つの違い Qikeru 学びを楽しくわかりやすく




平均値の求め方を教えて下さい Clear




最頻値 モード の求め方 高校数学 Youtube
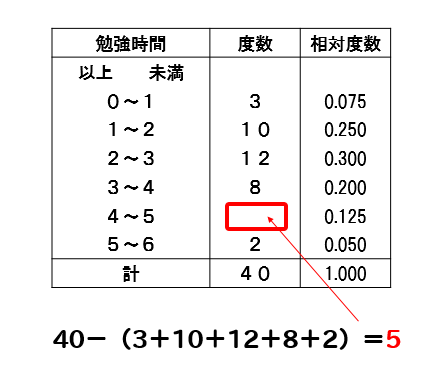



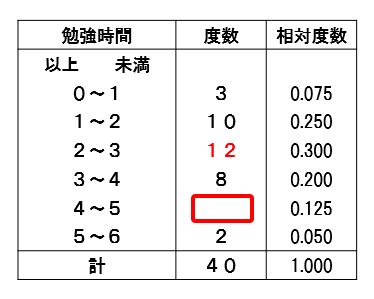
中学 相対度数の計算方法と問題はこれでバッチリ 数スタ




中学数学 平均値と中央値の3つの違い Qikeru 学びを楽しくわかりやすく




小学5年生の算数 平均の求め方 練習問題プリント ちびむすドリル 小学生
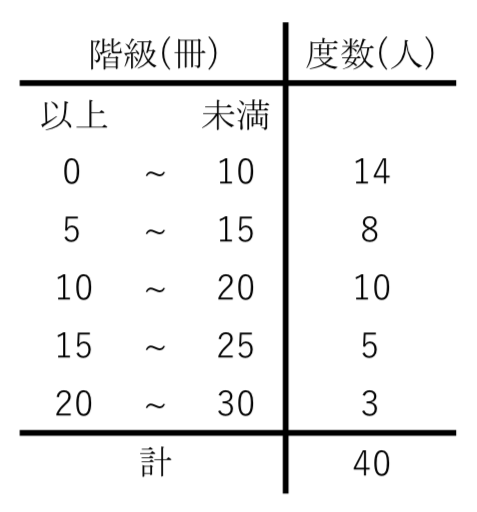



度数分布表から相対度数を求める 苦手な数学を簡単に




中1数学 中央値の求め方はこれでバッチリ 偶数 奇数の場合をそれぞれ解説 数スタ




中学数学 3分でわかる 平均値の出し方 Qikeru 学びを楽しくわかりやすく
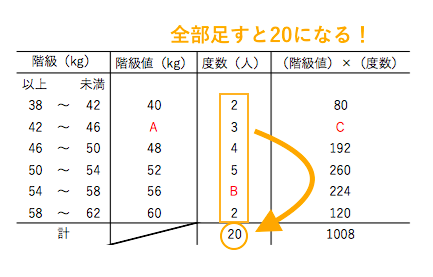



平均値と階級値について 苦手な数学を簡単に
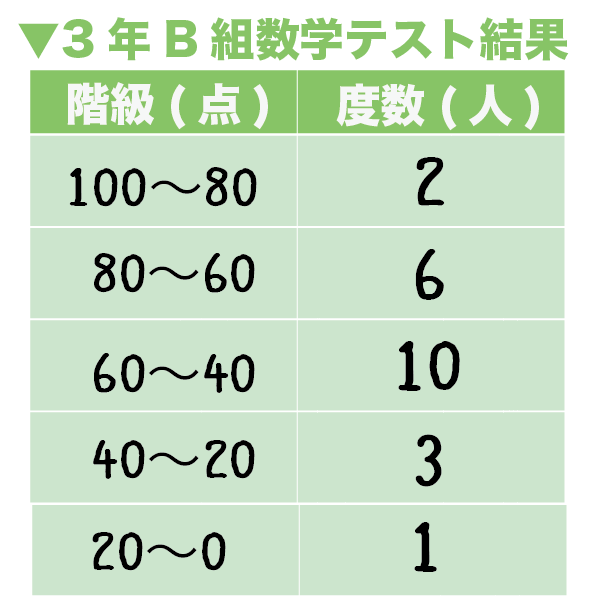



度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく



中学校数学 資料の活用 で学ぶ 中央値について質問です 資料が Yahoo 知恵袋




度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく
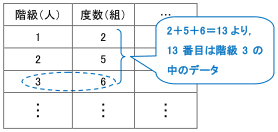



ヒストグラムが与えられたデータから 中央値を求める方法 数学 苦手解決q A 進研ゼミ高校講座



3分で分かる 平均値 中央値 最頻値の求め方をわかりやすく 練習問題つき 合格サプリ



データの分析を総まとめ 公式の覚え方や裏ワザ 重要記事一覧 受験辞典




平均値の求め方を教えて下さい お願いします Clear



中1数学 平均を文字式で表す問題を解説 数スタ



小6です 中央値がどこだか分からないので教えて下さい 全部で12個なので Yahoo 知恵袋



中学数学 代表値 平均値 中学数学の無料オンライン学習サイトchu Su



3分で分かる 平均値 中央値 最頻値の求め方をわかりやすく 練習問題つき 合格サプリ



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ




アとイの階級値を求めるのですが 求め方が分かりません Clear



1
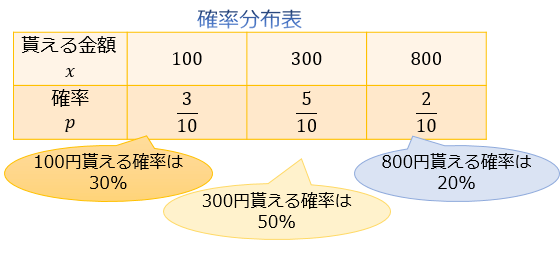



期待値の計算法と意味 その使い方と注意点 アタリマエ




中学数学 平均値と中央値の3つの違い Qikeru 学びを楽しくわかりやすく




中1数学 平均値 と 中央値 例題編 映像授業のtry It トライイット
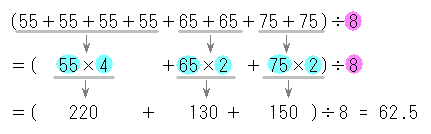



資料のちらばりと代表値 度数分布表からの平均値の求め方 中学数学 定期テスト対策サイト




中学数学 3分でわかる 平均値の出し方 Qikeru 学びを楽しくわかりやすく




中1数学 平均値 と 中央値 例題編 映像授業のtry It トライイット



0 件のコメント:
コメントを投稿